- 누텔라트리(hard)
- solved.ac
- boj23054
- 2023 Engineering Pair
- 27173
- K8s
- 2025acpc
- BOJ 30026
- 세그먼트 트리
- 백준
- 2023 SW - IT Contest
- 충남대학교 2023 SW - IT
- 알고리즘
- dx dy
- boj 30788
- 오일러투어트리
- BOJ 30027
- 수열과 쿼리 43
- CodeForces
- voronoi diagram
- Delaunay triangulation
- hhs2003
- BOJ 30028
- 느리게 갱신되는 세그먼트 트리
- 컴퓨터융합학부
- BOJ 31226
- BOJ17139
- 27114
- fortune's algorithm
- BOJ 30029
황현석 일지
Fortune's Algorithm 에 대하여 본문
더 좋은 퀄리티를 위해 글의 내용이 바뀔 수 있습니다.
며칠 동안, Fortune's Algorithm에 관한 글들을 찾아 읽으며, 원리와 그 작동방식.. 그리고 심각한 부동소수점의 오차 때문에 엄청 고생했다...
제일 답답했던 점은, 내 검색 엔진이 이상한 건지는 모르겠지만 이상하게만치, Fortune's Algorithm에 구현에 관한 자세한 설명이 있는 곳이 별로 없다는 것이었다.
물론 Fortune's Algorithm이 구현부가 굉장히 난해하고, 하나하나 짚고 넘어가면, 엄청나게 설명해야 할 것이 많기 때문에 웬만한 연산에 대해, 설명을 생략하는 글들이 대부분이었다...
무튼, 그래서... Fortune's Algorithm이 뭐냐...?
보로노이 다이어그램 (들로네 삼각분할)을 O(NlogN)에 생성하는 스위핑 알고리즘이다.
Fortune's Algorithm 은 기하학의 포물선과 교차점을 활용해 움직이는 BeachLine이라는 것을 만들고, 이벤트를 처리하는 스위핑 알고리즘이다.

사진을 가지고 조금만 설명해 보자면, 빨간색 선을 기준으로, 호들이 움직이는데, 이때 호들의 삭제가 일어난다. 그리고, 빨간색 선이 점들을 넘을 때, 호가 추가로 생기는데, 이때 호의 분리와 추가가 일어난다.

알고리즘은 위의 사진과 같은 Voronoi Diagram을 만드는 정보들을 O(NlogN)에 생성한다. 이를 활용하여 여러 문제들을 풀어 볼 수 있고, 심화 응용까지는 모르겠지만, 배우고자 하는 것이 이 정도로 디테일적인 요소가 많다면, 배울 것으로는 최고다.
나는 이 포스트에서 독자가, 빨간색 선(x축)을 기준으로, 호의 변화와 호의 추가 삭제를 언제 어떻게 해야 하는지 이해하고, 이를 이해한 상태에서 간단한 구현 몇 가지만, 맛보기로 이해하는 것을 목표로 글을 작성해보려고 한다.
아래의 내용을 매우 많이 참고했다.
너무 구체적인 설명까진 하지 않는다.
Fortune's Algorithm Notes from the book by de Berg
Fortune's Algorithm (for Voronoi diagrams) | Desmos
Point Event
"왜? 호를 관리하는 것이냐?? 왜? 하필 포물선들을 관리해야 하는 것이냐??" 라고 의문이 들 수 있다.
그냥 단순히, 스위핑 하는 x축을 기준으로 하여 x축을 이동시킬 때, 호들의 자취가 보로노이 셀의 영역이 되기 때문이다.

호(Arc)들을 관리할 것이고, 이 호들이 이루는 최외각 라인을 Beachline이라고 한다. 또한 현재 휩쓰는 x좌표를 SweepLine이라고 한다.
우리는 라인 스위핑을 진행하면서, 점을 만나게 되면, 그 점의 y좌표에 해당하는 beachline을 이루고 있는 호를 찾아서, 그 호를 기준으로 새로운 점을 초점으로 하는 Arc를 만들어 주면 된다. 이것을 전문용어로, Point Event가 발생했다고 한다.

왼쪽 사진에서 SweepLine이 점과 마주쳤을 때, 그 점을 초점으로 하는 호는 일직선 모양이다.. 그 후에, SweepLine이 진행 함에 따라, 기존에 호는 분할되고, 총 2개가 더 늘어난 모습이다.

사진 밖에 호가 하나 더 있고, 한 개의 호는 VerTex Event에 의해 삭제된 모습이다. 호를 이런 식으로 분할하고, 추가해 주면서 정렬되게 관리하는 게 우리의 목표가 될 것이다.
Vertex Event
호(Arc)가 삭제될 때를 전문용어로는 Vertex Event라고 부른다. 일단 호가 사라지는 장면을 시각화해서 관찰해 보자.

사진을 보면 알겠지만, 호가 지나간 영역이 보로노이 다이어 그램의 특정 점이 차지하는 셀의 영역이 되게 된다. 신기하지 않은가? 이게 우리가 SweepLine을 기준으로 BeachLine을 이루는 호들을 관리하는 이유이다!
잡설은 그만하고, 특징에 대해서 살펴보자.

호를 정렬하여 순서 있게 가지고 있다고 했을 때, 호가 사라질 때는 그 앞, 뒤의 호에 의해 영향을 받아 사리지게 된다.
사라지는 호는 영향을 주는 양 옆 두호를 이루는 초점들과 자기 자신의 초점의 외접원의 중심점에서 사라지게 되고, 이때 sweepLine 또한 외접원에 접해있는 것을 볼 수 있다. 이를 통해, 어느 지점까지 sweepLine이 진행돼었을 때, 삭제가 일어나는지 바로 유추해 낼 수 있고, Fortune's Algorithm에서는 이를 우선순위에 기록해 두어, 빨리 일어나는 이벤트 순으로 처리하게 된다.
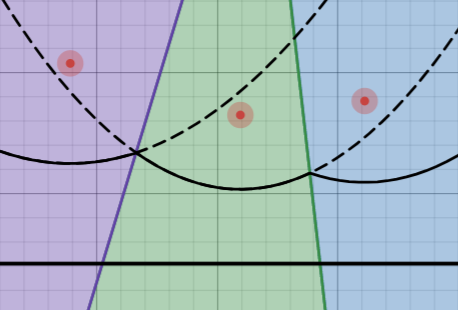
그렇지만, 모든 호가 사라지는 것은 아니라는 것을 알 수 있다. 당장에도 몇 가지 예외를 떠올릴 수 있다. ex) 세 초점이 평행하거나 양 옆의 호가 없을 수도 있다.
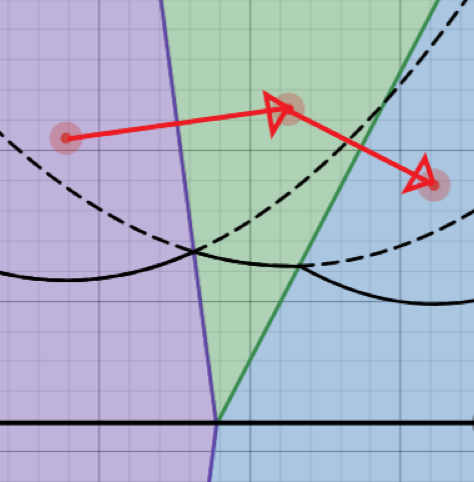
호가 사라지는 조건은, 호를 순서대로 하는 초점 3개에 대해, 그 방향이 시계방향이면 된다.
자 그러면, 우리는 호가 사라지는 조건과, 호가 사라지는 시간대 (sweepLine)를 알아냈으니까 Vertex Event 랑 Point Event랑 모두 우선순위에 넣고 돌리기만 BeachLine을 모든 sweepLine에 맞춰 완벽하게 구현해 낼 수 있다.
Implementation 구현
초기받은 점 순서로 점마다 인덱스를 붙여 놓는다. 호의 삭제가 이루어지면서, 점들 각각에게 정보를 저장해주어야 하는데, 점들을 미리 인덱싱 시켜놓으면, 편리하다.
그리고, 우리는 호(Arc)를 자료구조화 시켜, x축을 기준으로 스위핑 하면서 이 호(Arc)들을 관리해 줄 것이다.
본론부터 말하자면, 우린 호(Arc)에 다음 호(Arc)도 넣어서, 현재 스위핑 중인 X좌표에 따라, 어느 지점 Y좌표까지 이 호가 관리하는 영역인지 알 수 있게 할 것이다. 이런 식으로 하면, 우리는 새로운 점을 넣을 때, 어느 호에 넣어야 하는지 이분탐색으로 찾을 수 있다.
호 Arc 구현부를 보기에 앞서, 나는 웬만하면 정수연산으로 하려고 했기에, 정수 자료형인 Point와, 실수 자료형 Vector2D를 만들고 시작했다. 또한 EPS(epsilon)를 두어, EPS값만큼의 범위 안에 있는 두 수는 같다고 구현했다. 나는 EPS 귀찮아서 안 했다가.. 온통 터지고, 모든 부분에다가 EPS를 체크하는 불상사가 일어났었다.
부디, 독자들은 EPS를 두어, 사고를 미연에 방지했으면 좋겠다.
const long double EPS = 1e-11, INF = 4e18;
long double sweepX;
bool isSame (long double a, long double b) {
if (fabsl(a - b) <= EPS) return true;
return false;
}
struct Point {
long long x, y;
int idx;
Point () : x(0), y(0),idx(-1) {}
Point (long long x, long long y, int idx = -1) : x(x), y(y), idx(idx) {}
bool operator< (const Point& b) const {
if (x == b.x) return y < b.y;
return x < b.x;
}
};
struct Vector2D {
using vt = Vector2D;
long double x, y;
Vector2D () : x(0), y(0) {}
Vector2D (double x, double y) : x(x), y(y) {}
Vector2D (long double x, long double y) : x(x), y(y) {}
Vector2D (Point p) : x(p.x), y(p.y) {}
explicit Vector2D (pair<long double, long double> pr) : x(pr.first), y(pr.second) {}
long double dotProd (const vt b) const {
return x * b.x + y * b.y;
}
vt operator* (long double scalar) const {
return {x * scalar, y * scalar};
}
vt operator- (const vt b) const {
return {x - b.x, y - b.y};
}
vt operator+ (const vt b) const {
return {x + b.x, y + b.y};
}
bool operator< (const vt b) const {
if (isSame(x, b.x)) return y < b.y;
return x < b.x;
}
long double cross(const vt o) const {
return x * o.y - y * o.x;
}
vt rot () const {
return {-y, x};
}
long double size() {
return hypotl(x, y);
}
};
이제는 호를 만들어 보자. 코드포스 블로그에 있는 구현부를 대부분 가져온 것인데, Arc를 구조체로 하여, getY(x)를 기준으로 정렬시켜 놓는 자료구조형을 사용하는 것이 어떤 구현보다 굉장히 깔끔하고, 간단하다. 추후에, 점을 넣을 때, 어느 호를 분리하는지 한 줄로 찾을 수 있기 때문에, 아래와 같은 자료구조형을 사용하는 것을 추천한다.
독자가 직접... bbst를 만들면 말이 달라지지만... 굉장히 힘들 것이다..
호(Arc)는 호마다 고유한 id를 부여받게 한다. 호가 고유한 id를 부여받는 이유는 다음과 같다.
호(Arc)는 Vertex Event에 의해 사라지면, 사라지고 난 뒤의 앞, 뒤 호가 이어지는데 이때, 두 호의 vertexEvent 시점은 바뀌게 된다. vertexEvent 시점이 뒤로 늦춰지는 일은 없다.
따라서, 바뀐 vertexEvent 시점을 우선순위에 넣고 관리하게 되면, 더미값이 생기게 되는데 이 더미값을 없애기 위해서 전역에도 따로 기록해 둘 필요성이 생기게 된다. 따라서, 호마다 고유한 id를 부여하고 전역에 사라지는 시간을 기록하면서 관리할 수밖에 없게 된다.
int NOW_ID = 1;
struct Arc {
using pt = Point;
using vt = Vector2D;
// C : 초점, next : 다음 Arc의 초점
mutable pt c, next;
mutable int idx, id;
Arc (pt c, pt next, int idx) : c(c), next(next), idx(idx), id(++NOW_ID) {}
long double getY (long double x) const {
//다음 Arc가 없어서, 모든 지점커버.
if (next.y == INF) return INF;
if (c.x == next.x) return (long double) (c.y + next.y) / 2.0;
if (c.x == x) return c.y;
vt med = (vt(c) + vt(next)) * 0.5;
vt dir = (vt(c) - med).rot();
long double D = (x - c.x) * (x - next.x);
return med.y + ((med.x - x) * dir.x + sqrtl(D) * dir.size()) / dir.y;
}
bool operator<(const long double &y) const {
if (isSame(getY(sweepX), y)) return false;
return getY(sweepX) < y;
}
bool operator<(const Arc &o) const {
long double L = getY(sweepX);
long double R = o.getY(sweepX);
if (!isSame(L, R)) return L < R;
return c.x < o.c.x;
}
};
using beach = multiset<Arc, less<>>;
beach line;
다음은 Fortune's Algorithm의 전체적인 뼈대가 되는 함수이다. N개의 점을 입력받아, 인덱스도 기록해 놓고, points배열에 따로 담아 정렬한 다음에, sweepline알고리즘을 진행시킨다.
void solve(lint E = 1e6) {
cin >> N;
for (int i=0;i<N;i++) {
int x, y; cin >> x >> y;
pts[i] = Point(x, y, i);
points.push_back(pts[i]);
}
//dummy Value
points.emplace_back(0, E);
points.emplace_back(0, -E);
points.emplace_back(E, 0);
std::sort(points.begin(), points.end());
//dummy Value
line.insert(Arc(pt(-E, 0), pt(INF, INF), -1));
//Fortune's Algorithm
for (Point now : points) {
vertexEvent(now.x);
sweepX = now.x;
pointEvent(now);
}
circleEvent(8e18);
}
VertexEvent Implementation
void insertVoronoiPoint (Vector2D p, const vector<int>& indexes) {
for (int e : indexes) {
if (e < 0 || e >= N) continue;
voronoiPoint[e].push_back(p);
}
}
void vertexEvent (lint until) {
while (vertexQueue.size() && vertexQueue.top().x <= until) {
auto [x, it, id] = vertexQueue.top(); vertexQueue.pop();
// 삭제시간이 업데이트 되어서, 이건 더미 값이다.
if (deletedTime[id] != x) continue;
sweepX = x;
auto PREV = prev(it);
auto NEXT = next(it);
vector<int> receiver = {it->idx, PREV->idx, NEXT->idx};
vt res = circumcenter(vt(it->c), vt(it->next), vt(PREV->c));
insertVoronoiPoint(res, receiver);
line.erase(it);
PREV->next = NEXT->c;
getRemoveTime(PREV);
getRemoveTime(NEXT);
deletedTime[id] = INF;
}
}PointEvent Implementation
void pointEvent (Point p) {
//분리해야하는 호 c이다.
auto c = line.lower_bound(p.y);
if (isSame(p.y, c->getY(p.x))) {
auto b = line.insert(c, Arc(p, c->next, p.idx));
auto a = line.insert(b, Arc(c->c, p, c->idx));
vector<int> receiver = {p.idx, c->idx, c->next.idx};
auto res = circumcenter(vt(c->c), vt(c->next), vt(p));
insertVoronoiPoint(res, receiver);
deletedTime[c->id] = INF;
line.erase(c);
getRemoveTime(next(b));
getRemoveTime(b);
getRemoveTime(a);
} else {
auto b = line.insert(c, Arc(p, c->c, p.idx));
auto a = line.insert(b, Arc(c->c, p, c->idx));
getRemoveTime(c);
getRemoveTime(b);
getRemoveTime(a);
}
}
구현부를 이해 도움 참고용으로 올린 것이니.. 이해에 많은 도움이 되었으면 좋겠다.
에러가 난다면, 생각보다 예외케이스가 많다는 말을 하고 싶다. 사실 나는 이 PointEvent에 대해서 진짜 할 말이 무지하게 많다... VertexEvent는 실시간으로 호의 삭제시간이 바뀐다는 점에서 예외가 많을 것 같으나, 실상 호를 분리하고 삽입하는 PointEvent가 예외가 굉장히 많다.
PointEvent로 호가 추가 될 때, 추가된 호가 정렬된 상태를 잘 유지하고 있는지 잘 확인해 봐야 할 것이다.
호가 추가하자마자 삭제당하는 경우가 있다면, 추가자체를 하면 안 되며, 바로 빼주어야 한다. 또한, 호를 추가하는 시점에서 그 추가된 호의 모습은 일직선이다. 그전 호와 gety()가 같은데, 이것 또한 정렬이 잘 되어있는지 신경 써야 한다.
sweepX를 조금 빼는 것도 방법이긴 한데... 답은 없으니... Geometry's God에게 기도하는 수밖에 없다.
호가 삭제되는 시점을 잘 구하기 위해서는 beachLine의 호들이 정렬된 상태를 유지시켜 주는 것이 제일 중요하다.
전체 구현은 아래에 올려 두었다.
DataStructures/fortune/fortune.cpp at main · Hy3ons/DataStructures
'알고리즘 풀이' 카테고리의 다른 글
| BOJ 30788 - Sakura Reflection (0) | 2024.10.28 |
|---|---|
| BOJ 27577 - Everything is A Nail (0) | 2024.10.01 |
| 2024 SW - IT Contest 문제 풀이 (1) | 2024.09.29 |
| BOJ 1146 - 지그재그 서기 (0) | 2024.08.06 |
| BOJ 9616 - 홀수 정사각형 (0) | 2024.08.03 |



