- 2023 SW - IT Contest
- 27173
- 느리게 갱신되는 세그먼트 트리
- 누텔라트리(hard)
- 냅색
- 수열과 쿼리 43
- fortune's algorithm
- BOJ 30026
- BOJ 31226
- BOJ 30029
- 백준
- 2023 Engineering Pair
- BOJ 30028
- 오일러투어트리
- BOJ17139
- Dynamic Programming
- BOJ 30027
- Sakura Reflection
- boj23054
- Delaunay triangulation
- dx dy
- boj 30788
- 충남대학교 2023 SW - IT
- 27114
- hhs2003
- 세그먼트 트리
- 알고리즘
- 컴퓨터융합학부
- voronoi diagram
- CodeForces
알고리즘 일지
Virtual. Educational Codeforces Round 166 (Rated for Div. 2) 본문

오늘도 어김없이 버츄얼을 한판 돌렸다. 바쁘거나 그러지 않으면, 밤 10시쯤에는 버츄얼을 무조건 돌리고 있다.
오늘은 성적이 역대급이지만, 버츄얼이라 그런지.. 오히려 좀 슬프다..
A. Verify Password
이 문제는 보자마자 좀 짜증이 났다... 저걸 언제 다 구현하지...
그래서, 문제에서 요구하는 데로 Comparator를 하나 만들고, 정렬시킨 다음 똑같은지 비교했다.
B. Increase/Decrease/Copy
$A$ 배열의 원소를 1, -1씩 연산해서 $B$배열을 만드는 최소 연산 횟수를 묻고 있다.
근데 $B[N]$도 주어져서 $A$배열의 원소를 하나를 복사해 와야 한다.
최대한 가까울 때 복사해서 만들면 된다.. 간단한 구현이다.. A문제보단 쉬웠다. 구현만 하면 됐다.
근데 한번 틀렸다.
C. Job Interview
사장이, 프로그래머, 테스터를 각각 $N$명, $M$명 뽑는다.
$i$번 직원부터 $N+M+1$번 직원까지 순서대로 $N+M$명, 뽑는데, 사장이 그리디 한 방법으로 프로그래밍 능력이 더 좋으면 프로그래머로써, 테스터 능력이 좋으면 테스터로 먼저 배치한다.
나중에, TO가 없으면, 그냥 남는 자리에 배정하는 식이다. 문제는 각각, $i$번 직원이 없을 때, $N+M$명의 직원을 뽑으면, 총회사의 능력치가 어떻게 되는지를 묻고 있다.
일단 TO가 없어 억울하게 반대자리에 앉은 최초의 직원을 기록해 놓는다.
TO가 없어 억울한 직원들은 없어져도 직업이 바뀐 직원이 없다.
자기 능력대로 들어온 직원들은 사라지면, 그 자리 TO가 하나 생긴 것이기 때문에, TO가 없어 억울하게 반대자리에 앉은 최초의 직원은 자신의 본직을 찾을 수 있다.
D. Invertible Bracket Sequences
이 문제를 일단 '('을 $1$ ')'를 $-1$이라고 배열에 작성한 다음 Prefix Sum을 구해주고, 이산적인 그래프 형식으로 변환시켜 생각해 봤다.
일단, 문제에서 주어진 괄호식은 정규 괄호식이므로, 그래프 모양은 다시 0으로 돌아가는 모양을 띌 것이다.

우리가 쿼리 $[l, r]$을 날려, 괄호를 바꾼다는 것은, 이 그래프의 변화를 반전시키는 것과 같다.
반전시켰는데, 0을 뚫고 -1로 간다는 것은 그 결과가 정규 괄호식이 아님을 의미한다.
반전시켰을 때, 0을 뚫고 아래로 안 내려가는 지점을 여러 곳 찾으면 된다.

아래와 같이 파란색 구간을 반전시키면, 다시 원래대로 값이 안정적으로 돌아와 -1 로가지 않는 정규 괄호식이 된다.
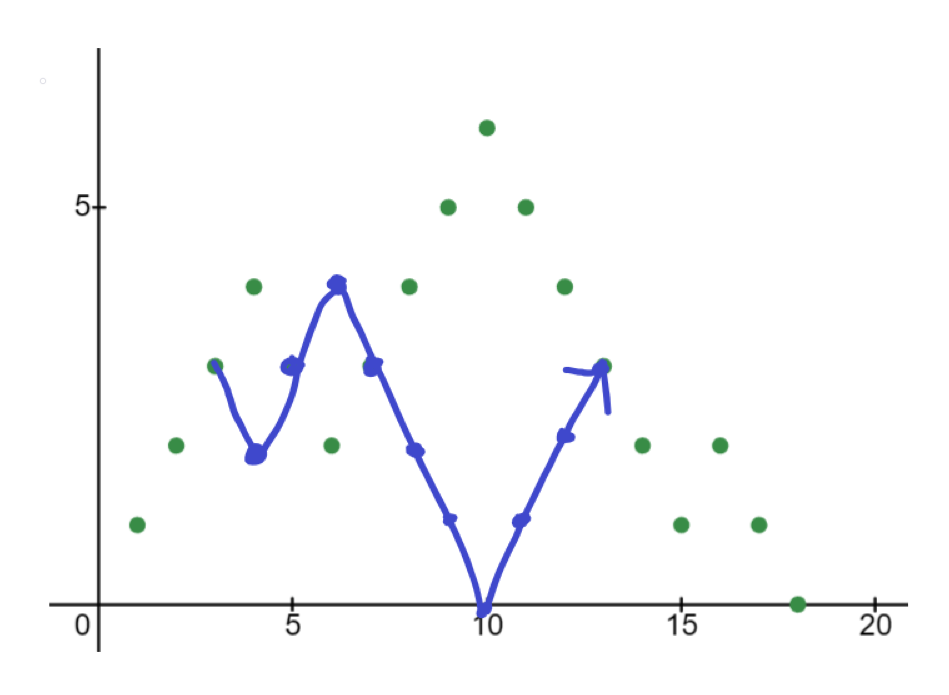
다음 구간도 반전시킬 수 있다.
이런 식으로 같은 y축에서 반전시킬 수 있는 구간들을 $K$개 모은 다음, $\bigg\lfloor \frac{K (K-1)} {2} \bigg\rfloor$ 을 해주면서 답을 기록해 주면 된다.
-1을 뚫는 걸 검사하려면 max Segmet tree를 이용하면 된다. 나는 킹갓 Splay Tree 템플릿으로 밀었다.
E. Splittable Permutations
아직 풀지 못했다. 문제에서 주어진 대로 최대한 조건에 맞게 수열을 만들어 본다고 하자. 일단 설명하기 어렵고 복잡하지만 다 건너뛰고 중요한 사실 몇 가지만 나열하겠다.
첫 번째론, 주어진 연산을 통해, 일부 순서는 구성을 할 수 있다는 점이다.
나는 이 순서를 구성할 때, 구조체를 만들고 쪼개서 둘로 나누고 하는 식으로 만들었다.
그렇게 만들어진 순열을 $\text{A}$라고 하자.
우린 이 순열 사이에 $max(A_i, A_{i+1}) $ 미만의 값들을 어떠한 순서라든지 넣을 수 있다는 점이다.
그렇게 우리는 이제 수들이 들어갈 수 있는 경우를 굉장히 적절히 잘 카운팅 해주면 된다.
일단 순열 사이에 어떠한 값 미만의 값들을 전부 넣을 수 있다. 당연히 이 값들은 아직 배정되지 않은 값이다.
즉, 어떠한 수 $K$가 어떤 수열 사이에 들어갈 수 있다면, $K$보다 작은 어떠한 숫자도 들어갈 수 있다는 점이다.
자, 그러면 큰 수 부터 넣는다고 가정하겠다. 현재 만들어진 모든 경우의 수를 $V$라고 하겠다.
어떠한 수 $K$가 $m$개의 자리에 들어갈 수 있을 때, $K$수를 배정하고 나서 만들어진 경우의 수는, $V \times m$이다.
그 후에는, $K-1$을 배정한다고 해보자. 그럼 몇 개의 자리가 생긴 걸까????? $K$가 들어가며, $K$의 앞쪽 뒤쪽으로도 자리가 생겼기 때문에, $m$, 배정할 수 있는 자리는 무조건 1 늘어나게 된다.
#include<bits/stdc++.h>
using namespace std;
const int MAX = 303030;
const int MOD = 998244353;
int N, Q;
struct node{
node *l, *r, *p;
int value = 0;
};
node *arr[MAX];
int pre[MAX], L[MAX], R[MAX];
vector<int> vc;
void init (node *n) {
if (n->value != 0) {
vc.push_back(n->value);
return;
}
init(n->l);
init(n->r);
}
node *root = new node();
void f (node* p, int l, int r) {
arr[l] = new node();
arr[r] = new node();
arr[l]->value = l;
arr[r]->value = r;
arr[l]->p = p;
arr[r]->p = p;
p->value = 0;
p->l = arr[l];
p->r = arr[r];
}
int main () {
cin >> N >> Q;
for (int i=0;i<Q;i++) {
cin >> L[i];
}
for (int i=0;i<Q;i++) {
cin >> R[i];
}
f(root, L[0], R[0]);
for (int i=1;i<Q;i++) {
if (arr[L[i]]) {
f(arr[L[i]], L[i], R[i]);
} else {
f(arr[R[i]], L[i], R[i]);
}
}
init(root);
for (int i=0;i<vc.size()-1;i++) {
pre[max(vc[i], vc[i+1]) - 1]++;
}
pre[vc[0]-1]++;
pre[vc.back()-1]++;
typedef long long lint;
lint ans = 1;
lint fv = 0;
for (int i=N;i>=1;i--) {
fv += pre[i];
fv %= MOD;
if (!arr[i]) {
ans *= fv;
ans %= MOD;
fv++;
}
}
cout << ans;
}
'코드포스' 카테고리의 다른 글
| Educational Codeforces Round 168 (Rated for Div. 2) (0) | 2024.07.31 |
|---|---|
| Pinely Round 4 (Div. 1 + Div. 2) (0) | 2024.07.29 |
| Codeforces Round 959 (Div. 1 + Div. 2) 업솔빙 (0) | 2024.07.19 |



