- dx dy
- CodeForces
- 백준
- boj23054
- Delaunay triangulation
- 오일러투어트리
- 수열과 쿼리 43
- fortune's algorithm
- 알고리즘
- BOJ 30027
- 느리게 갱신되는 세그먼트 트리
- 27173
- voronoi diagram
- 컴퓨터융합학부
- K8s
- 2025acpc
- 누텔라트리(hard)
- 2023 Engineering Pair
- 27114
- 세그먼트 트리
- boj 30788
- BOJ17139
- BOJ 30028
- BOJ 30026
- 충남대학교 2023 SW - IT
- 2023 SW - IT Contest
- solved.ac
- BOJ 30029
- BOJ 31226
- hhs2003
황현석 일지
2023 SW - IT Contest 운영진 후기 본문

안녕하세요. 참가자 여러분들! 2023 SW - IT Contest에 운영진으로써 참여하게 된 황현석이라고 합니다.
이번 운영진 체험(?) 비스무리한 활동을 하며, 얻어가는 것도 배워가는 것도 많은 뜻깊은 좋은 시간이었다고 생각합니다.
대회 당일날 딱봐도 군인처럼 생긴 이상한 아저씨가 한명 돌아다니고 있었는데요!.. 저였습니다..
그냥 휴가를 나왔는데, 대회 일정이랑 겹쳐 있어서 운이 좋았네요!!... 오랜만에 학교 공기도 쐐고.. 흐음~~
공기가 별로 좋지는 않았어요..

1등이.. 22학번 최약체라... 그중 최약체가 1등을 하게 되었군요. 제가 빨리 복귀해야겠어요.
그리고 이번에 1등한 최약체는 내년에는 군대에 있겠지만, 출제에 참여 할 수 있도록 제가 강제 조취하겠습니다.
저는 23. 1. 17일날 입소하여 군인이 되었기 때문에, 운영진으로 활동 할 때도 군인 신분이었습니다. 따라서, 저의 운영진으로써의 역할은 되게 제한적이었습니다.
저는 군대에서는 폰으로 밖에 주로 활동을 하지 못했기에, 문제 제작과, 검수 쪽을 주로 담당하였는데요. 폰으로, 코딩을 하고, 문제를 만들고 검수를 뛰는 것은 굉장히 정신적으로 이롭지 못한 것 같습니다.

이번에 쓰일 문제를 준비하면서, 운영진들의 머릿속에서 거의 50개에 달하는 문제 아이디어와 풀이들이 등장하였는데요. 제가 준비한 문제는 정당성 증명도 어려워서 보류 된 문제도 있고, 굉장히 어려운 문제였지만, 검수 과정에서 쉬운 풀이가 등장해, 보류 된 문제도 존재합니다 ㅜㅜ.
이렇듯, 문제를 준비하면서, 어떤 문제가 좋은 문제고, 문제는 또 어떤식으로 만들어지며, 문제를 잘 만들기 위해서 생각해 방향 등등 많이 생각해보는 시간을 가진 것 같습니다.
그렇게 깨지고 깨진 결과... 저는 "잃어버린 순수" 라는 제목으로 된 트리 문제를 하나 만들게 되었습니다.
이 문제는 처음엔, 저의 지적 호기심인.. 경로로 트리를 덮는데 필요한 경로의 숫자를 알아내기 에서 시작 되었습니다.
그렇게 숫자는 금방 알아냈지만, 실제로 해를 구성하는 경우도 가능한지 고민해 보게 되었고, DFS 탐색을 통한 트리에서의 greedy 매칭을 통해, dp 형식으로 매칭이 가능함을 알게 되었습니다.
또한 다른 여러가지 방식으로 해를 구성할 수도 있는데요..!! 이건 따로!!.... 아래 풀이에서 만나 뵐게요..!
운영하면서, 시온형이 이번에도 역시나 굉장히 영혼을 갈아 넣었는데요!! 이번에는 그나마, 다른 운영진들의 군대 전역과... 22학번의 신성이 유입되어... 그나마... 어깨의 짐을 덜어드리지 않았나..(?) 싶네요...
우진이 형도 사무적인 부분에서 굉장히 도와주셨는데요! 문제 출제, 티켓과, 입장 수속, 문서 작성의 대부분의 일을 도맡아 주셨습니다.. 고생 많으셨습니다..
지훈이 형도 문제 출제와, 검수, 에디토리얼 작성 쪽에서 일을 맡아주셨습니다. 형도 고생 많이했어요!
준원이도 대부분의 문제의 검수, 사짜 풀이 제작과, 문제 제작과 스페셜 저지 제작에서 힘을 써주었습니다.
대회 날 입국해서 달려온 유진 누나도 사무적인 부분에서 힘써주셨습니다. 고생많으셨어요.
이번 기회에 운영진으로써, 옆에서 관람(?) 비슷한 걸 하면서 대략 대회가 어떻게 만들어지는지 알 수 있었는데요. 정말 귀중한 경험이었다고 생각합니다.
SW - IT Contest를 운영진으로써 참가하는 것도 많은 경험이 된다고 생각합니다. 이번 운영 경험하면서 느낀게 있는데, 운영진 허들은 그렇게 높지 않다는 것입니다. 저는 문제를 푸는 것밖에 못했었지만, 이번 기회에 전반적으로 다 성장한 것 같습니다.
운영진들 티어가 낮으면 골드부터, 높으면 다이아 하위까지 였는데요...
실력이 높고, 티어가 높아야만 운영진을 하는 건 아닙니다. 여러분들 부담 가지지 말고 적극적으로 운영진 신청 많이 해주셨으면 좋겠어요!
아래부터는 제가 검수했던 문제를 하나씩 보며, 풀이와 저의 생각 있었던 일들을 풀어 나갈려고 합니다!
없는 문제는.... 제가 풀이와 정당성 증명을 하지 않은 문제입니다... 풀어보지도 않았어요...
30018. 타슈
타슈... 이건 시온형이 평소에 타고 다니는 애마 같은 것인데요. 이건 수식으로 하면 정답은
$\sum_{i = 1}^{N} max(b_i - a_i, 0)$ 이 되게됩니다. 이건 이중포문으로 구현해도 시간복잡도 와는 관계없이 다 맞을 수 있어서, 비전공자 분들 대상으로 낸 문제입니다.
30019. 강의실 예약 시스템
배열을 하나 선언하여, 종료시각을 저장해 두면, 풀 수 있는 문제입니다. 그동안 들어온 쿼리를 나이브하게 탐색하는 행위를 막기위해 시온형이 굉장히 노력하셨습니다. 빠른 입출력을 사용해야 통과하는 문제인데요... 힌트까지 드렸는데... 그냥 푸시는 분들을 보며 안타까운 마음이 들었습니다.. 풀이는 맞는데 ㅜㅜ....
30021. 순열 선물하기
백준을 풀다보면, 대부분 애라토스테네스의 체(Sieve) 라는 것을 배우게 됩니다. 대부분이 체를 이용하여, 소수 판별을 하고, 나이브한 백트래킹을 사용하여 문제를 해결 하셨는데요.. 사실 그건 정해가 아닙니다 ㅜㅜ..... 물론! 나이브한 백트래킹을 저희는 정해로 인정하고, 여러분들이 정답을 제출 하는 것을 예상하여, 낮은 난이도로 책정하였습니다.
사실, 1부터 $N$까지의 합은... 합성수잖아요? $(N > 2)$
30022. 행사준비
저는 이 문제를 굉장히 어려운 문제로 알고 있었습니다. 교환논법의 스탠다드가 되는 문제인데요.. 다만 접근하게 쉽게 만들어서 그런지, 제 평가의 절하의 절하의 절하를 당해 지금은 실버에 안착해 있네요..
상점 1에서 100원에, 상점2에서 300원에 판다면, 상점1에서 구매하나, 상점 2에서 구매하나, 100원의 비용은 들게 됩니다.
그럼, 상점 1에서 0원에, 상점2에서 200원에 파는 걸로 바꾸어서 생각해 볼 수 있어요.
이런 식으로 모든 물건에 적용해보면, 한 물건은 0원, 한 물건은 가격이 0이상이겠죠.
그럼 어떤 물건부터 0원에 원하는대로 골라야 최대한 이득을 볼까요? 그건 당연히 상대적으로 비싼 물건을 피해 사는게 이득이겠죠? 그렇게 두 물건의 차이를 우선순위로 하여, 기회를 다 소진하고, 소진한 기회는 그냥 남은 반대편 상점에 기회에 모두 사용하며 문제를 풀면 됩니다.
30023. 전구 상태 바꾸기
아.. 전구.. 시온형이 굉장히 좋아하는 주제인데요.. 작년에는 전구 상태 뒤집기라는 문제가 나왔었습니다..
25634번: 전구 상태 뒤집기 (acmicpc.net)
저번년도 문제를 참고하여 만든 이번 상태 바꾸기는 그저, 색깔을 정해 그 색깔을 만들어 보기만 하면 되는 문제였습니다.
저는 이 문제를 검수하진 않아서, 정확한 풀이와, 정당성 증명에 대해 모릅니다... ㅜ.ㅜ
확실히, 문제 구현과, 풀이는 쉽지만, 정당성 증명을 어떻게 해야 될 지 모르겠는 면이 있었는데요.
참가자들이 그냥 건너 뛰고 푼 이유는 여기에 있지 않을까? 생각해봅니다..
제가 참가자 였어도 이 문제는 건너뛰고, 풀었을 것 같아요..
30024. 옥수수밭
우선순위 BFS를 통한 탐색을 진행하여 문제를 풀면 됩니다. 가장자리를 두번 pq에 넣는 실수를 저지르지만 않는다면, 이문제를 쉽게 푸실 수 있었을 거에요!
저는 검수 할 때, 우선순위에 많이 넣어도, 우선순위 안에서 방문한 지점을 다시 꺼냈을 때, continue 하게 만들어서, 문제는 되지 않았었네요! ^^
30025. K의 배수
K의 배수... 이번 대회에서 이 문제가 악명이 제일 높았다고 생각합니다. PS에 경험이 많은 분들이라면 아시겠지만, 이건 당연하다 싶이 DP에요 라고 소리를 지르고 있는 문제인데요. 그렇기에, 오히려 빨리 풀릴 수 있을 것 같았지만, 상당히 참가자 분들이 어려워 하는 문제가 아니였을까? 싶네요..
$dp[i][j]$ 를 $i$번째 자릿수 까지 수를 만들었을 때, 나머지가 $j$인 경우의 수라고 합시다.
그럼 점화식은 나머지가 $j$인 경우에서 수를 새롭게 붙였을 때, 변화한 나머지로 전이시키면 됩니다.
제가 이 문제를 만들지도... 점화식을 확실하게 잘못쓰겠네요.. 코드에서 어디로 경우의 수가 이동하는지 보시는게 더 도움될 거라고 생각합니다.
이 문제는 아트하게 구현하는게 좀 힘든데요. 저는 수를 뒤에서 부터 만들어서 구현했습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
#include <iostream>
#include <vector>
#define MOD 1000000007
using namespace std;
int N, M, K;
vector<int> A, B, nums;
int main (){
cin >> N >> M >> K;
int s;
A.resize(K, 0); B.resize(K);
for(int i=0;i<N;i++) {
cin >> s;
if(!s && M==1)continue;
nums.push_back(s);
A[s%K]++;
}
int ten = 10 % K;
for(int i=1;i<M;i++) {
fill(B.begin(), B.end(), 0);
for(int j = 0;j<K;j++) {
for (int n : nums) {
if(i==M-1 && n == 0) continue;
int t = (ten * n + j)% K;
B[t] += A[j];
B[t] %= MOD;
}
}
swap(A, B);
ten *= 10;
ten %= K;
}
cout << A[0];
}
|
cs |
이 코드는 폰으로 솔루션을 작성했던 코드인데요, 이런 식으로, A와 B배열을 swap 하면서, 토글링(toggling) 기법을 사용해서 문제를 해결 했었습니다. 이 문제는, 테스트 케이스를 만들 때, 애먹지 않았던 문제가 아닐 까 싶네요..
이 문제에서 고군분투한 상위권 참가자들!! 수고 많이하셨습니다!!


$a_i \not= a_j \ (i \not= j)$ 입니다. $i$ 도시에서 $a_i$로 갈 수 있다고 할 때, 이를 directed Graph 로 환원하여 그립시다.
그럼 문제 조건에 의해, $a_i$ 도시를 가르키는 간선은 $i$ 도시가 유일합니다. 그럼 directed Graph의 모양은 꼬리에 꼬리를 무는 사이클을 이루는 모양이 될 것입니다.
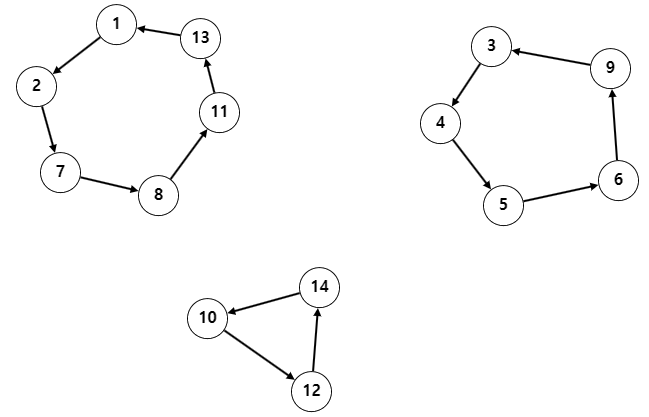
결국 이 간선방향을 교환하여, 사이클을 하나로 통합해야 하는데요. 사이클이 $K$개 일 때, 적어도 $K-1$개의 간선 교환을 통해, 사이클을 하나로 만들 수 있습니다. 이때, 이 비용을 최소화 해야 합니다.
문제를 풀 때, 이 문제에서 정답이 될 수 있는 최소 비용에 대해 생각해 보셨나요? 이 문제에서, 될 수 있는 최소 비용은 $K-1$이 됩니다.
간선의 교환에는 비용이 최소 1이상이 들고, 간선은 최소 $K-1$번 교환해야 하기 때문입니다.
두 사이클을 합칠 때, 비용이 1인 것을 찾을 수 있을까요? 당연합니다. 다른 두 사이클에 포함된 두 지역 사이의 번호가 1 차이나는 경우를 무조건 발견 할 수 있습니다.
이것을 UnionFind를 통해, 구현하여, 해를 구성할 수 있습니다.
이 문제에 도전한 배인수 학생에게 경의를 표합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
int N, d[202020], p[202020];
vector<pair<int, int>> s;
int getP(int n) {
if (p[n] == n) return n;
return p[n] = getP(p[n]);
}
void unite (int n1, int n2) {
int p1 = getP(n1);
int p2 = getP(n2);
p[p1] = p2;
}
int main () {
cin >> N;
iota(p, p+202020, 0);
int k;
for(int i=1;i<=N;i++) {
cin >> k;
unite(i, k);
d[k] = i;
}
int answer = 0;
for(int i=1;i<N;i++) {
if(getP(i) == getP(i+1)) continue;
answer++;
unite(i, i+1);
s.emplace_back(d[i], d[i+1]);
swap(d[i], d[i+1]);
}
cout << answer << ' ' << answer << '\n';
for(auto z : s) cout << z.first << ' ' << z.second << '\n';
}
|
cs |


이 문제는 상위권 참가자들의 실력구분을 위해 만들었는데요. 저희도 문제 검수하면서, 혹시나 이걸 푸는 참가자 분이 있다면, 즉석해서 특별상을 만들지 않았을까 생각해봅니다.
일단 단순 BFS는 $O(NM)$ 이므로 시간초과입니다. 참가자 분들중 제출한 소스코드는 거의 단순 BFS를 응용한 탐색이었습니다ㅜㅜ.
이 문제는 상대적으로 $N$이 작은데요! 이것을 이용하여 문제를 풀어봅시다.
시간을 알아내야 하는데요... 갑자기 훌쩍 발상의 도약이라고 느끼실 수도 있어요..!
특정 시간 이후로 화원에 모든 칸에 꽃이 피어있기 때문에 이분적으로 화원의 상태를 구분 할 수 있습니다. 그렇기 때문에 시간에 대해 이분탐색을 해봅시다. 이것을 파라매트릭 서치.. 매개변수를 통한 이분탐색이라고 부릅니다.
특정 시간 $t$에 대하여, 화단의 상태를 어떻게 빠르게 체크할 수 있을 까요?
$N$이 상대적으로 작다는 것을 이용하여, 각 행에 대해, 꽃으로 가득 차 있는지 검사해봅시다.
검사하는 행 $n$와, 꽃 $K$개에 대하여, 꽃은 선분으로 표현 할 수 있고, 이는 sweeping 기법을 활용하여, $O(K \log K)$에, 행 $n$가, 꽉 차있는지 확인 할 수 있습니다.
이러면 총 시간복잡도는 $O(N K \log K \log (N+M))$입니다.
사실 이 시간복잡도는 아슬아슬한데요... 조금 관찰을 더하면 시간복잡도를 줄일 수 있습니다.
꽃을 미리 열에 대해 정렬합시다.
시간 $t$에 대해, 각 행 $n$에 대해, 선분으로써, 영향을 주는데요. 꽃을 미리 정렬해 놧다면, 선분이 정렬 되게 들어옵니다. 선분은 기존에 있던 선분을 다 포함하게 들어올 수도 있고, 뒤에 들어오는 선분이 포함 될 수있는데요. 이걸 stack을 이용하여, 관리하면, 각 행에 대해 검사를 $O(K)$로 끝낼 수 있습니다.
그럼 시간 복잡도는 $O(NK \log(N+M))$가 되게 됩니다.


아... 제가 만든 문제인데요.. 상당히 실수한 부분이 많습니다 ㅜㅜ. 기존 문제와 유사하단 점도 있고 제대로 활동할 수 없는 군인의 한계가 드러나는 문제인 것 같습니다 ㅠㅠ.
이 문제는 정답으로 향하는 풀이가 굉장히 많은 문제입니다. 여러분께는 제가 관찰한 DFS 통한 트리에서 그리디 매칭을 통해 리프노드를 매칭하는 것을 알려드리겠습니다.
리프노드의 개수를 $K$개라고 합시다. 이때 그럼 최소 간선을 $\lceil \frac{K}{2} \rceil$개 추가해야합니다.
최소 간선 개수만으로 트리의 모든 정점을 사이클에 포함 시킬 수 있을 까요?
가능합니다.
DFS를 통해, 리프노드를 끌어올리면서, 각 노드를 경유하게 그리디하게 매칭합니다. 이 때, 리프노드를 1개 혹은 2개를 남기면서 끌어올리다 보면, 트리의 모든 정점을 리프노드가 거슬러 올라가게 했으므로, 모든 정점을 포함 하게 매칭 할 수 있습니다.
DFS를 시작한 루트 정점에서는 특수한 예외 처리를 해주면, 바로 정답으로 풀 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
|
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int N, u, v;
typedef pair<int, int> box;
vector<int> load[101010], dp[101010];
#define first from;
#define second target;
void dfs (int node, int prev = 0) {
vector<int> two, one;
bool ends = true;
for(int next : load[node]) if (next != prev) {
dfs(next, node);
if(dp[next].size() == 1) {
one.push_back(next);
} else {
two.push_back(next);
}
ends = false;
}
if(ends) return;
//case work
if(two.size() == 1) {
if (!one.empty()) {
int twoo = two[0];
int another = one[one.size()-1];
one.pop_back();
cout << dp[another][0] << ' ' << dp[twoo][1] << '\n';
dp[twoo].pop_back();
two.clear();
one.push_back(twoo);
} else {
for (int i : dp[two[0]]) dp[node].push_back(i);
return;
}
}
// Now no two 1 case
for(int i = 1;i<two.size();i++) {
cout << dp[two[i-1]][0] << ' ' << dp[two[i]][1] << '\n';
}
if(!two.empty()) {
int siz = two.size();
dp[two[0]][0] = dp[two[0]][1];
dp[two[0]].pop_back();
dp[two[siz-1]].pop_back();
one.push_back(two[0]);
one.push_back(two[siz-1]);
}
int up = one.size() % 2 == 0 ? 2 : 1;
for(int i=0;i<up;i++) {
dp[node].push_back(dp[one[one.size()-1]][0]);
one.pop_back();
}
for(int i=0;i<one.size();i+=2) {
cout << dp[one[i]][0] << ' ' << dp[one[i+1]][0] << '\n';
}
}
int main () {
cin >> N;
for(int i=1;i<N;i++) {
cin >> u >> v;
load[u].push_back(v);
load[v].push_back(u);
}
int start, ano = 0;
for(int i = 1;i<=N;i++) {
if(load[i].size() == 1) {
dp[i].push_back(i);
ano++;
start = i;
}
}
ano = ano / 2 + (ano &1);
cout << ano << '\n';
dp[start].clear();
dfs(start);
for(int i=0;i<dp[start].size();i++) {
cout << start << ' ' << dp[start][i] << '\n';
}
return 0;
}
|
cs |
하지만 이것 말고도, 무작위화를 통한 매칭도 가능합니다. 혹은 오일러 투어를 이용하여, 적당한 순서의 정점끼리 매칭하는 것도 하나의 방법입니다. 그렇지 않으면, 하나의 경로를 붙잡고, 경우를 따져 경로교환을 진행하는 것도 하나의 방법입니다. 혹은 HLD를 이용하여, 그 경로들을 다 관리하는 것도 하나의 방법입니다.
이렇게 이 문제는 굉장히 풀이가 많아서 괜찮은 문제지만, 이미 만들어진 문제가 있기에.. 저는 솔직히 공부했다는 마음도 있지만, 백준에는 크게 기여하지 못했다는 마음이 큽니다..
다음에는 노력하여, 더 어렵고 교육적인 문제를 만들도록 하겠습니다.


하하하! 마지막 문제네요! 이 문제는 작년에 만든 도미노 넘어뜨리기에서 $N$만 20만으로 키운 문제입니다!
25633번: 도미노 넘어뜨리기 (acmicpc.net)
제가 만든 문제에 치명적인 사짜 풀이가 발생하여, 급하게 어려운 문제를 만들다가, 시온형이 제안한 도미노 넘어뜨리기의 강화판입니다. 시온형이 문제를 제안했었고, 저는 풀 수 있을 것 같아서 열심히 풀다가 결국 문제로 나오게 되었습니다..
참가자 여러분들이 그냥 보지도 않았다고 했는데요... 저는 대회에서 이런 어려운 문제가 나와야 참가자 여러분들이 일반 어려운 다이아 문제보다는 그래도 호기심을 가지고 접근 하실 수 있을 것 같고, 결국 이런 문제를 풀어서 실력을 높일 수 있다고 생각합니다.
도미노 넘어뜨리기는 그냥 한 도미노를 계속 시작지점으로 삼아서 최대한 길게 만들어 나가는 브루트포스 형식의 문제 였다면, 도미노 수열문제는 그 문제에서 관찰을 추가적으로 요구하는 문제가 아닌가 싶네요!
도미노 넘어뜨리기는 단순하게 생각해도 되지만, 도미노 수열은 dp식이나 정리를 통해 Naive 하게 생각하여 관찰을 통해 최적화를 한다음, 자료구조를 사용하여 마무리하는 문제입니다.
풀이
도미노 수열들을 만들어 가면서 문제를 풀어봅시다. 어떻게 만들거냐면, $a_i$를 첫 번째 수부터 마지막까지 순서대로 덛붙힐 수 있는 모든 도미노 수열에 덛붙히면서 도미노 수열들을 관리할 것입니다.
이때 도미노 수열들은 길이랑 합만 관리 할 것입니다.
관찰 1. 존재하는 도미노 수열들에 $a_i$를 덛붙힐 수 있으면 덛붙히는게 무조건 이득이다.
- 덛붙히면 다음 이어지는 $a_{i+1}$가 커도 덛붙힐 수 있으므로 덛붙히는게 무조건 이득입니다.
관찰 2. $a_i$를 덛붙힐 수 있는 도미노 수열이 존재 할 경우, $a_i$로 시작하는 도미노 수열을 새롭게 만들지 않아도 된다.
- $a_i$를 덛붙힐 수 있는 도미노 수열이 존재 할 경우, 관찰 1에 의해 그 도미노 수열에 붙히는게 이득이기 때문에 붙여야 합니다. 이때, $a_i$가 붙여진 도미노 수열은 $a_i$만 있는 도미노 수열보다 합도 크고, 길이도 길기 때문에, $a_i$로 시작 하는 도미노 수열은 절대로 정답이 될 수 없습니다.
관찰 3. $a_i$를 덛붙힐 수 없는 수열이 존재 하지 않을 경우, $a_i$로 시작하는 도미노 수열을 무조건 만들어야 한다.
- 이후에 나오는 $a_j \ (i < j)$ 에 대해, 모두 $a_i \ge a_j $를 만족 할 수 있기 때문이다. 이 경우에는 $a_i$로 시작하는 도미노 수열이 정답이 될 수도 있다.
관찰 4. $a_i$ 를 추가 할 때, 관찰 1과 관찰 3의 경우 중 한 가지 경우만 무조건 일어난다.
- 관찰 1의 경우가 일어 나지 않았다면, 덛붙힐 수 없는 수열이 존재 하지 않는 다는 경우 이므로, 관찰 3의 경우 이다.
- 관찰 3의 경우가 일어 나지 않았다면, 덛붙힐 수 있는 수열이 존재 한 다는 것이므로, 관찰 1의 경우이다.
관찰 1 에 의해, 도미노 수열의 합이 $a_i$이상인 모든 도미노 수열에 $a_i$를 덛붙여야 합니다.
이때, 도미노 수열들은 길이와 합만 관리 할 건데, 해당 되는 모든 도미노 수열에 합을 모두 $a_i$를 더하고, 길이를 1씩 늘릴 수 있을 까요?
도미노 수열들을 관리 할 때, 합 오름차순 으로 정렬 된 채 관리 할 수 있을까요?
관찰 5. $a_i$가 추가 될 때, 관찰 4에 의거하여, 도미노 수열을 관리하면, 도미노 수열들을 정렬 된 채 관리 할 수 있습니다.
- 도미노 수열들을 정렬 된 채 관리하고 있을 때, 관찰 1에 의거하면, 정렬 된 도미노 수열들은 합이 $a_i$ 이상인 모든 도미노 수열들의 합은 모두 단조 증가 함으로, 정렬 된 상태를 유지합니다.
- 관찰 3에 의거할 땐, 합이 $a_i$ 이상인 도미노 수열이 없고, 합이 $a_i$ 인 도미노 수열이 새롭게 생기게 됩니다. 이 때, 도미노 수열이 가장 크므로 맨 뒤에 붙이면 정렬 된 상태를 유지 합니다.
도미노 수열들을 정렬 된 채 관리 할 수 있으면, 합이 $a_i$ 이상인 도미노 수열을 찾고 그 앞까지 모두 적용 시키면 됩니다.
이를 Lazy Segment Tree 자료구조를 사용하여, 행할 수 있습니다.
도미노 수열들의 합을 관리하는 Lazy Segment Tree는 구간 최대 합을 구해놓으면, 그 트리 안에서 받은 인자값을 가지고 이분탐색 하듯이 내려 갈 수 있습니다.
그렇게 Upper Bound를 찾고, 길이를 모두 1씩, 합을 모두 $a_i$씩 늘리는 구간 쿼리를 진행하면 됩니다.
이때, 길이는 실시간 으로 파악 하지 않아도 되므로, 업데이트에 $O(1)$, 마지막 갱신에 $O(N)$이 걸리는 자료구조를 사용해도 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
|
#include <iostream>
#define MAX 202020
using namespace std;
int N;
typedef long long lint;
lint treeW[MAX*8], lazy[MAX*8], prefix[MAX], arr[MAX];
void push (int n, bool p) {
if(!lazy[n]) return;
if(p) {
lazy[n<<1] += lazy[n];
lazy[n<<1|1] += lazy[n];
}
treeW[n] += lazy[n];
lazy[n] = 0;
}
int finder (int n, int s, int e, int l,int r, lint t) {
push(n, l != r);
if(r < s || e < l || treeW[n] < t) return 0;
if(l == r) return l;
int mid = l + r >> 1;
int temp = finder(n << 1, s, e, l, mid, t);
if(temp) return temp;
return finder(n << 1 | 1, s, e, mid+1, r, t);
}
void updateW (int n, int s, int e, int l, int r, lint w) {
push(n, l != r);
if(r < s || e < l) return;
int mid = l + r >> 1;
if(s <= l && r <= e) {
lazy[n] = w;
push(n, l != r);
return;
}
updateW(n<<1, s, e, l, mid, w);
updateW(n<<1|1, s, e, mid+1, r, w);
treeW[n] = max(treeW[n << 1], treeW[n << 1 | 1]);
}
lint answer () {
lint ans = 0;
for(int i=0;i<N;i++) {
prefix[i+1] += prefix[i];
ans = max(ans, prefix[i+1]);
}
return ans;
}
int main () {
cin >> N;
for(int i=0;i<N;i++) {
cin >> arr[i];
}
lint mx = 0, V=0;
for(int i=0;i<N;i++) {
if(mx < arr[i]) {
V++;
mx = arr[i];
prefix[V]++;prefix[V+1]--;
updateW(1, V, V, 1, N, arr[i]);
} else {
mx += arr[i];
int idx = finder(1, 1, V, 1, N, arr[i]);
prefix[idx]++;prefix[V+1]--;
updateW(1, idx, V, 1, N, arr[i]);
}
}
cout << answer();
}
|
cs |
난이도는 기존 세그먼트 트리 다이아 5 문제의 기조를 반영하였습니다.
Lazy Segment tree 를 알고 있는 분들이라면, 쉽게 구현 할 수 있는 문제니, 한번 씩 다들 풀어 보셨으면 좋겠습니다.
운영에 도움을 준, BaekJoon, SolvedAc, startLink, 충남대학교 공과대학 총학생회에 감사를 드립니다.
대회를 성공적으로 마무리 할 수 있게 해준 참가자들에게도 또한 감사를 드립니다.
후원을 추가로 해준 전진호형과, utilForever님께 감사를 드립니다.
운영진들도 모두 고생하셨습니다.
'황현석 어록' 카테고리의 다른 글
| 객체 지향 설계 프로그래밍 C++, 중간 겸 고찰 (4) | 2025.10.20 |
|---|---|
| C의 Array Pointer 에 대한 고찰 및 응용 그리고 연습 (1) | 2025.06.20 |
| 충남대학교 2025 1학기를 마치며... (3) | 2025.06.18 |
| 2025 ACPC 참가 후기 (3) | 2025.05.27 |
| 알고리즘, 템플릿을 정리하고 있습니다. (0) | 2024.07.18 |

